As noted in Part IV of this series (see link below), determining the potential life of a machine can be relatively complex and, thus, call for some detailed experimental studies. In this series installment, we will review the potential life of the insulation on a 50-hp, 1800-rpm motor at constant speed and load. For variable applications, such as those in EV (electric vehicles), a machine-learning (ML) or statistical study across speeds and loads using different operator and environmental information would be applied.
(For a more detailed approach, see my 2014 IEEE Electrical Insulation Conference Paper, “Evaluating Reliability of Insulation Systems for Electric Machines,” at Evaluating Reliability of Insulation Systems for Electric Machines – MotorDoc LLC )
As noted in Part IV, Equation 4, the base thermal life of the insulation system (L) at the experimental accelerated aging temperature (155 C, for this example) is calculated at room temperature (25 C). Base hours at accelerated aging totaled 220, at which time testing was stopped, whether the insulation failed or not. In this study, 80% of the insulation materials survived to 220 hours. The base life at room temperature is calculated as shown in Example 1 below, assuming that the slope of the experimental curve is 2.9:
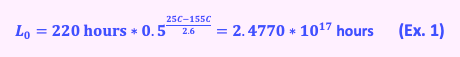
In effect, the electric motor insulation system could sit at room temperature in a static atmosphere for 2.828*1013years, which, of course, is theoretical and does not include any external factors. Without outside sources, if the motor had Class F insulation (155 C) operating at 120 C, the expected life would be 283.3 years (calculated by replacing 25 C with 120 C) 2.4817*106 hours. Since this is an unusually long expected life, we need to start considering other life impacts (multi-factor aging), starting with electrical stress, from Part IV, Equation 6 and using the operating temperature of 120 C, as presented in Example 2 below:

The expected time using electrical stress and operating at 120 C with an insulation system that is resistant to 12,000 volts would be 5.215*105 hours, or 59.5 years of continuous operation at 120 C.
If we include thermal shock in our experiment, as shown in Part IV, Equation 6, there will be 20 hours of thermal shock applied from the 220 hours, which is depicted in Example 3 below:
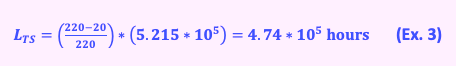
The result is a drop to 4.74*105 hours, or 54 years. If we also review the vibration impact from a study and find that 80% of machines fail at 180 hours when 160 hours of excessive vibration due to unbalance or misalignment (simulated), which results in Example 4 below. Failure is determined when the winding fails expected test results.

The added high vibration reduces the life from 54 years to 6 years. The vibration/shock for the experiment is set at 0.4 in/sec for this impact. An adjustment to 0.2 in/sec results in 11 years for the insulation system from the experimental data.
If contamination is included, such as moisture and grease, at 50 hours during accelerated testing and failure is defined as low insulation resistance at 99 hours, by, applying Equation 9 in Part IV, the expected life would be as found in Example 5 below:

With all conditions above, our motor could operate continuously for 2.7 years. These conditions, from an experimental standpoint, are extreme and provide a threshold for the point where 20% of machines would fail.
Based on our original data, the B20 of the machine starts at 59.5 years. Then it’s adjusted based on operating environment. However, a combination of thermal shock, vibration, and contamination drops the expected life to 2.7 years. In such a case, testing and predictive-maintenance (PdM) inspections would be able to identify when the different conditions become part of the expected life of the insulation system.TRR
Click The Following Links For Parts I And II Of This Short Series
“Part I, The Possibilities Of Probability: In Reliability And Predictive Maintenance” (Nov. 6, 2021)
“Part II, The Possibilities Of Probability: In MTBF” (Nov. 15, 2021)
“Part III, The Possibilities Of Probability: In Failure Curves And RUL” (Nov. 20, 2021)
“Part IV, The Possibilities of Probability: In Non-Linear Failure Curves And RUL,” (Nov. 27, 2021)
ABOUT THE AUTHOR
Howard Penrose, Ph.D., CMRP, is Founder and President of Motor Doc LLC, Lombard, IL and, among other things, a Past Chair of the Society for Maintenance and Reliability Professionals, Atlanta (smrp.org). Email him at howard@motordoc.com, or info@motordoc.com, and/or visit motordoc.com.
Tags: reliability, availability, maintenance, RAM, electrical systems, predictive maintenance, Artificial/Augmented Intelligence, AI, Machine Learning (ML), Internet of Things, IoT, P-F Curve



