Years ago, I had to learn about the associated filter-related terms “Beta Ratio” and “Beta Efficiency.” I had read that we can calculate fluid-filter efficiency after ascertaining the Beta Ratio.
By convention, Beta Ratio is a measure of a filter’s efficiency. The term was introduced to give filter manufacturers and end-users an accurate and representative comparison of available filter media. It is determined by a multi-pass test that establishes the number of particles upstream from the filter that are larger than the micron rating of the filter. That number is then divided by the number of particles downstream from the filter larger than the micron rating of the filter. The following figure and example will demonstrate the concept of Beta Ratio quite clearly.
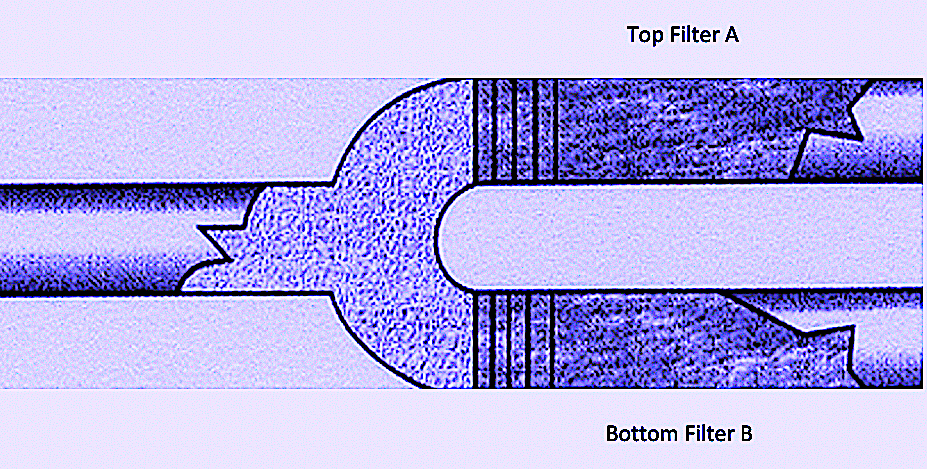
Suppose that the upstream condition for both filters (Top Filter A and Bottom Filter B) is 200 particles larger than 3 microns, and assume that we find the downstream condition of Top Filter A is 100 particles larger than 3 microns. In that case, the Beta Ratio = 200/100 = 2.
Next, let’s say we find that the downstream condition of Bottom Filter B is 1 particle larger than 3 microns. In that case, the Beta Ratio = 200/1 = 200.
Based on the above example, we would understand there are 200 particles upstream from each of the two filters that are larger than 3 microns in size. A filter having a lower Beta Ratio is less efficient because it allows more particles to pass through. Again, based on the above example, we would understand that while Top Filter A allows 100 particles to pass through, only one particle is allowed to pass through Bottom Filter B.
Accordingly, the Beta Ratio for Top Filter A is given by Beta = 200/100 = 2, which is a less efficient value. The Beta Ratio for Bottom Filter B is given by Beta = 200/1 = 200, which is a more efficient value.
Next, we use the following equation to determine the efficiency value of a filter, known as Beta Efficiency.
Beta Efficiency = (Number of upstream particles) minus (Number of downstream particles),
all divided by (Number of upstream particles),
where the particle size is greater than a specified value of N microns.
The relationship between Beta Ratio and Beta Efficiency can thus be represented as:
Beta Efficiency = 1 – (1/Beta Ratio)
For example, a filter with a Beta Ratio of 20 would have an efficiency of 1 – (1/20) = 95%. A filter with a Beta Ratio of 2 has a Beta Efficiency of 1 – (1/2) = 50%. The higher the Beta Ratio, the higher the Beta Efficiency. And here’s why you would want to know all this:
- High efficiency usually means greater propensity for high pressure drop.
- Overcoming this pressure drop means elevated power requirements.
If bearing clearances are 10 microns in size, filtering out all except 1-micron-sized particles may not make economic sense for the simple reason that these particles will not cause a measurable decrease in bearing life.TRR
Editor’s Note: Click Here To Download A Complete List Of Heinz Bloch’s 22 Books
ABOUT THE AUTHOR
Heinz Bloch’s long professional career included assignments as Exxon Chemical’s Regional Machinery Specialist for the United States. A recognized subject-matter-expert on plant equipment and failure avoidance, he is the author of numerous books and articles, and continues to present at technical conferences around the world. Bloch holds B.S. and M.S. degrees in Mechanical Engineering and is an ASME Life Fellow. These days, he’s based near Houston, TX. Email him at heinzpbloch@gmail.com.
Tags: reliability, availability, maintenance, RAM, fluid filtration, fluid flow, fluid handling, filter media, pumps, bearings
.



